The sale price of housing is not its economic price

The sale price of homes is not the economic price of housing. Prices, in the economic sense, are the relative cost of consuming newly-produced goods and services.

The economic price of housing is therefore the rental price. It represents the price of being housed today. The rental price is what goes into consumption price indexes. It goes into the national accounts to represent housing service production. It is what standard economic theory says is the price of housing.

The sale price of a house represents the purchase of a perpetual stream of housing services. In essence, you are buying the right not to have to rent a home from someone else.

Why is it important that the sale price of a house is not its economic price?

Because sale prices of housing can rise while their economic price falls. The economic price of housing translates into a sale price via other factors.

So how is the sale price of housing determined?

The asset pricing model 

The sale price of homes is determined in much the same way that the price of other rights to future income streams; the asset pricing model.

Converting the value of a flow of uncertain future income flows into a capital value today is an imperfect procedure, relying on estimates of risk, uncertainty and growth prospects. But we can for now ignore these judgements to demonstrate how the ingredients that create an asset price from the value of an income stream fit together.

Housing asset prices can be reflected by the following formula.

Asset price = (gross rent - ongoing costs) / (risk-adjusted return + property tax rate - growth expectations)

There are hence five ingredients in asset prices, of which only one is the economic price in the form of the annual rent. This is why housing asset prices can diverge so significantly from rental prices.

Let us go through each ingredient.

• Gross rent is the total amount a renter would have to pay to occupy the home for a period. It is the economic price of housing. 
• Ongoing costs include upkeep of the house—the maintenance required to sustain its current quality over time (depreciation)—as well as other ownership costs such as taxes and fees that are not levied as a fixed rate on the property value. 
• The risk-adjusted return is the rate of return buyers are will to pay for that property based on their assessment of market alternative investment returns, and the relative rate of risk of buying this house. For example, if you can get a 5% return on you money in the bank from interest, and buying this house is seen as much risker than bank deposits, then this return will be something above 5%, say 8%. 
• The property tax rate is the rate per dollar on the total property value that is required to be paid in taxes. In most US cities and states, property taxes are levied on the full asset value of the house and land, whereas in other places like Australia, these taxes are levied only on the land value component. I have adopted the US approach here for simplicity. 
• Growth expectations reflect the rate at which much buyers expect rents or prices to rise in the near future. For example, you may buy a house to avoid paying $20,000 per year rent, but rents might be rising at 5% per year. Next year, your current house purchase saves you $21,000, and it saves you $22,000 the following year. 
• We are going to simplify this model for now by pretending that growth expectations are zero. This avoids the part of the recipe that leads to big swings in the value of housing that usually self-correct over time. We will also pretend that the risk-adjusted return is best captured by the prevailing mortgage interest rate. Once you see the logic if the model, you can easily tweak these assumptions yourself to see their effect on asset prices. 

The cost of buying vs the cost of renting

Here is an example of the asset pricing model in action. A house has the following characteristics.

Rent is $20,000 per year
Ongoing costs are $5,000 per year
Mortgage rates (risk-adjusted return) are 6%
The property tax rate is 0.5%
Growth expectations are zero.

The sale price of this home will be roughly $231,000 according to the asset pricing formula [(20,000-5,000)/(0.06+0.005) = $231,000].

What this means is that you will be equally well off economically—i.e. you will spend the same each year—if you borrow the full house price amount and buy it as you would be renting it. We can add up the annual costs of buying to seeing that it is the same as renting.

Interest = $13,850 ($231,000 x 0.06)
Ongoing costs = $5,000
Taxes = $1,150 ($231,000 x 0.005)
Total = $20,000

You might notice that I have only considered the interest cost of a mortgage, not the total repayment. But paying the principle of the house is not an economic cost. It is an asset investment just like paying listed equities is an investment, not an economic cost.

Our homebuyer in this situation is paying a $20,000 economic cost of housing. But if they pay the principle of their loan over 30 years, the mortgage repayment is $16,780 per year, or $2,930 more than the interest alone. Their out-of-pocket expenses are $22,930, but that include the purchase of $2,930 of housing equity each year.

The effect of low interest rates 

Most of the change in housing sale prices over the past decade are not due to the economic price of housing as the chart below shows. Rents have been flat in Australia, and in many cities globally, while sale prices have grown enormously. 

If recent sale price changes are not due to rents, then they must be due to one of the other ingredients in the asset pricing model.

We can eliminate the ongoing costs of upkeep. Construction costs have been steady, and fixed fees and charges also have seen little variation. Property tax rates are also relatively unchanged, at least in Australia. Note also that higher property taxes reduce asset prices.

We are now down to two factors—the risk-adjusted return and growth expectations.

It could be that buyers of housing have increased their expectations of rental growth. Though after a decade of flat or falling rents, rental growth expectations should certainly have been curtailed, rather than increased.

This leaves only the interest rate. To me, this is the big story for housing prices over the past two decades globally.

We can take our previous example dwelling where we calculated its value to be $231,000 when mortgage interest rates were 6%. Now, mortgage interest rates are closer to 2%. At what price does buying cost the same as renting at this much lower rate?

Again assuming zero growth expectations, our asset pricing formula is (20,000 - 5,000) / (0.02 + 0.005) = $600,000. That’s a 160% increase in sale price, while the economic price of house remains unchanged.

We can check this calculation to ensure that the economic cost of buying at this price remains the same as before.

Interest = $12,000 ($600,000 x 0.02)
Ongoing costs = $5,000
Taxes = $3,000 ($600,000 x 0.005)
Total = $20,000

Notice that the interest paid on a mortgage is actually lower in this case, though the annual taxes are higher due to the higher sale price.

What about property taxes? 

At lower interest rates the effect of property taxes on asset prices increases. Let us compare the sale price of our example house in two different jurisdictions—one with a property tax rate of 0.5%, and one with a property tax rate of 2%.

First, we can see the effect of property taxes in our high 6% interest rate scenario. Recall that the asset price with a 0.5% property tax rate was $231,000. If we now put a 2% property tax rate in our asset pricing equation, the house is worth $187,500. Compared to this high-tax region, the asset price of the same house in a low-tax region will be 23% higher. That is a huge difference. Yet the economic price of housing is the same.

In the low interest rate scenario our house was worth $600,000 in the 0.5% low property tax area. If we plug in a 2% property tax rate and a 2% interest rate we get a value of $375,000 in the high-tax region. The sale price is now 60% higher in the low tax area for the same economic price of housing. The low interest rate environment amplifies the price effect of different property tax rates.

We can see the components of the economic price in the high property tax area in the low interest rate scenario below. 

 
Interest = $7,500 ($375,000 x 0.02)

Ongoing costs = $5,000
Taxes = $7,500($375,000 x 0.02)
Total = $20,000

We can therefore use the asset pricing model to predict that the recently-announced reductions in property tax rates in Harris County (Houston) will fuel price growth in the current low interest rate environment. We can also predict that states like Texas, with comparably high property tax rates (often 2% and above) will have even greater housing asset price divergence compared to regions with low (sub 1%) property tax rates.

Predicting strange price differences

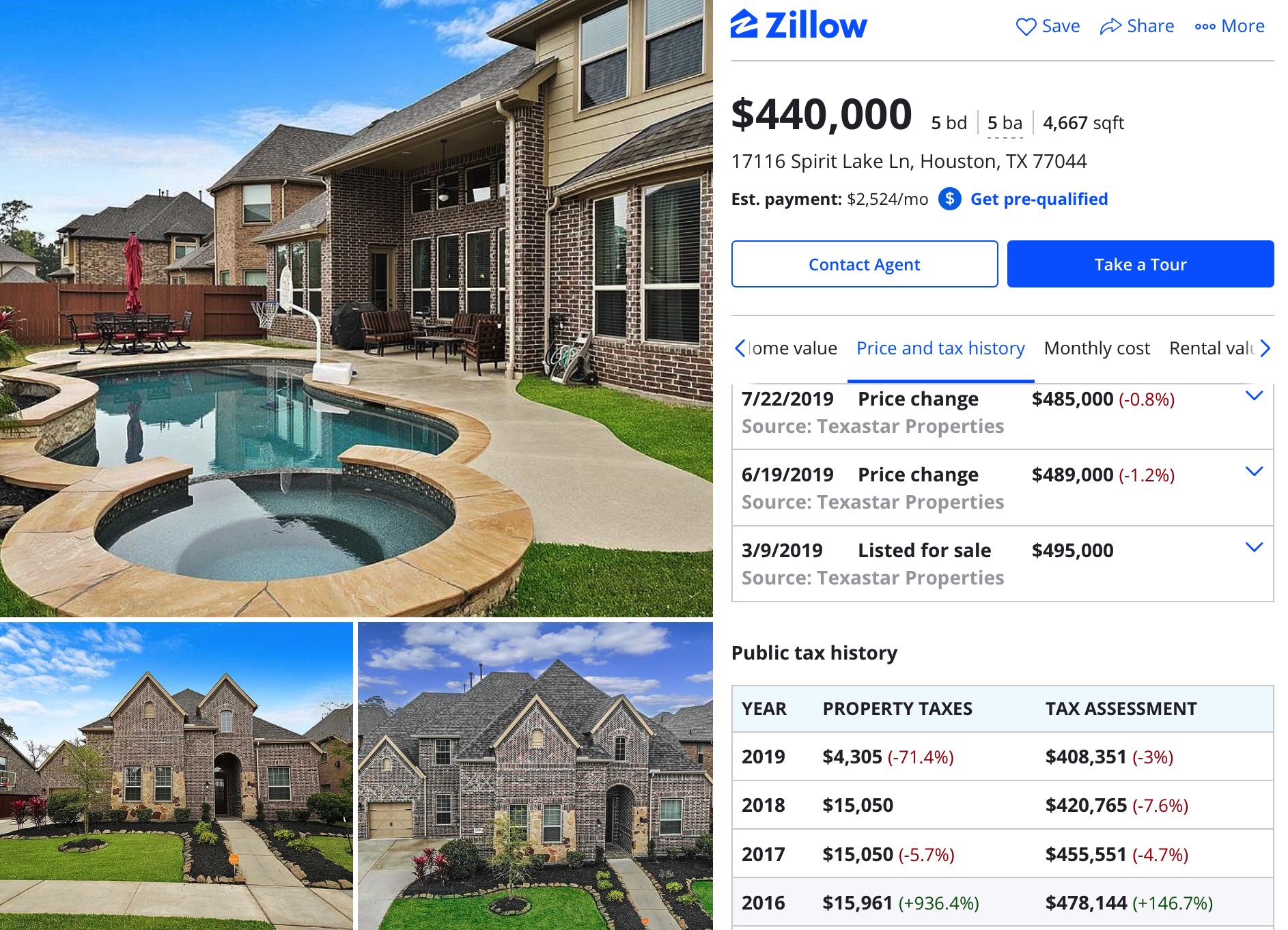
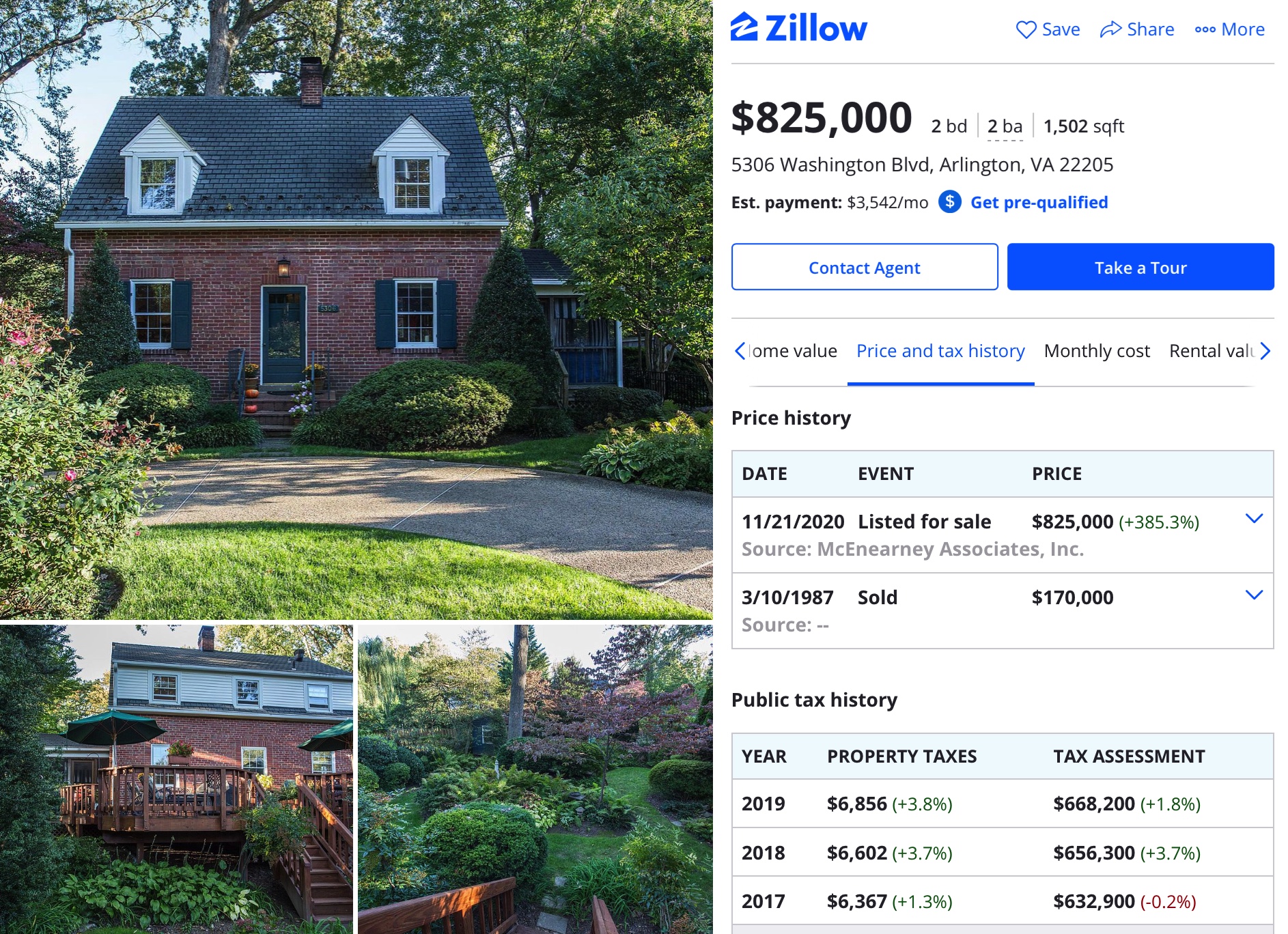
Strange house price differences make more sense through the lens of asset pricing.

Here is an example of the types of strange price differences commonly noted. Here are two houses where the asset price seems unrelated to the quality or size of the dwelling.

House 1

House 2

Can asset pricing make sense of the fact that the much smaller home is worth nearly double the much larger one?

It can.

We can even acknowledge that the economic price of the larger home is much higher, despite location difference. But this does not have to translate into a higher asset price.

The large home, House 1, might have the following characteristics.

Gross rental per year: $40,000
Property tax rate: 3%
Ongoing/upkeep per year: $10,000

The high upkeep costs (aka depreciation) come from its size and features, such as the pool. Notice that property taxes are around $15,000 per year for this dwelling, which is over 3%.

The smaller home might have the following characteristics.

Gross rental per year: $30,000
Property tax rate: 0.8%
Ongoing/upkeep per year: $5,000

Notice the much lower property taxes and upkeep costs. This has a big effect when converting the economic price into an asset price.

I’m going to apply a 2% mortgage interest rate to the asset pricing formula to show what price to expect for these two homes.

House 1
Price = $40,000 - $10,000 / (0.02 + 0.03) = $600,000

House 2
Price = $30,000 - $5,000 /(0.02 + 0.008) = $893,000 

Although the economic price, the rent, is 33% higher for House 1, this doesn’t translate to asset prices. In fact, House 2 is worth nearly 50% more than House 1 under these conditions (my price estimate is a bit on the high side for both as I’m using a round 2% and ignoring any difference in other asset pricing factors). 

Remember, at these prices, each house has the same economic price for buying as it does for renting. House 1 also has an economic price 33% higher than House 2. 

House 1
Interest = $12,000 ($600,000 x 0.02)
Ongoing costs = $10,000
Taxes = $18,000($600,000 x 0.03)
Total = $40,000

House 2
Interest = $17,900 ($893,000 x 0.02)
Ongoing costs = $5,000
Taxes = $7,100($893,000 x 0.008)
Total = $30,000

If you are not looking at housing sale prices through an asset pricing lens, these strange house price differences will only seem to get worse as we enter a super-low interest rate period. Many people will mistakenly attribute the difference in asset price to physical and regulatory factors, like zoning. But if these factors do affect housing, the must do it through their effect on the economic price, the rent, not the asset price.
____________________________
Next post: Why is the share of income spent on housing so stable over time in almost every place?

Why does land have a positive value?

Modern housing economists, following in the footsteps of Ed Glaeser, seem to think that the market price of land should be zero. Land only has a positive value because of artificial scarcity generated by zoning laws.

I am not making this up. This is exactly the theory Glaeser has been pushing for two decades.

According to this view, housing is expensive because of artificial limits on construction created by the regulation of new housing. It argues that there is plenty of land in high-cost areas, and in principle new construction might be able to push the cost of houses down to physical construction costs.
…
this hypothesis implies that land prices are high, not due to some intrinsic scarcity, but because of man-made regulations.

If the price of housing is only the construction cost, that means that the price of the land (location) for housing is zero. It seems a little crazy when you say it this way. Which is why it is usually said in a more sensible sounding “internal logic of my economic model” kind of way. If the input costs to land are zero, and markets are competitive, then the price will converge to input costs. Add in some hedging words, and you begin to sound profound.

But although the model is internally consistent, it is clearly the wrong model. Why?

Land is not a newly-produced good or service, which is the domain of typical economic models of markets, where prices converge to a point that “clears” markets.

Land is instead a perpetual property right to a long-lived scarce asset that can generate income flows. Just like an ownership share of a company, land represents a share of ownership of the finite three-dimensional space.

No one would argue that because there are no input costs for Apple or BHP shares—creating new shares is a legal manoeuvre with essentially no input costs—that competitive trading of these shares will eventually lead to a zero price.

Yet the same argument is thought to be valid when the asset class is land. Maybe if we had public exchanges for land ownership, people would see the commonalities more than they do.

But why can’t land markets be competitive and converge to a zero price? The reason is that the land titles system creates a monopoly over space.

What is puzzling to me is that this monopoly feature of land markets was widely understood issue in the 19th century. It triggered the invention of the Monopoly board game (originally called the Landlord's Game) which demonstrated the monopoly problems inherent to the land titles system and their distributional effect.

Even now, the issue is clear to many who study it. Here’s an entertaining take on the land titles system, and here’s an academic exposé on the issue.

But it remains hidden in the housing supply debate. It is the dog that does not bark in the mystery of rising home prices.

I want to try a new way to communicate the monopoly characteristic of land. The table below shows two ways in which space can be allocated by property titles—either not carved up, with one lot containing all the dwellings on a region, or carved up so that each dwelling sits on its own lot, representing a share of the space. Call it a lot share.

The table also shows two ways in which a property title (a lot or lot share) can be owned—either by a single person or by many people. 

If we have one giant lot that contains all the dwellings in a region, and that lot is owned by a single person, then that clearly makes the land market a monopoly. This is a situation similar to company towns, where a company builds housing on land near a natural resource or mine to provide local accommodation for its workers. 

Even if that single large lot was owned by many people, such as through a corporate structure, a co-op, or another legal mechanism, it would still be seen as a monopoly. 

Although many people own a share of the total space, the space is only one land lot, one property title, so the number of owners does not matter. All the owners’ interests are the same. The monopoly outcome is expected. Even if there are 100 dwellings, with each occupant owning a one-one-hundredth share in the company, it is still a monopoly. 

Now let’s carve up ownership a different way. Rather than owning a one-one-hundredth share of a company that owns the single lot containing all one-hundred dwellings, each household ones a one-one-hundredth share of the lot. Rather than subdivide the company structure, the lot structure is subdivided into lot shares.

Each household still owns a one-one-hundredth share of the space. 

Does this change to the legal structure of ownership change the economic outcome? If so, why?

In Ed Glaeser’s model world, switching the ownership structure of this area so that each household went from part-owner of the entity that owns the space to part-owner of the space would immediately crash the price of land to zero.

This is internally consistent with his model—land has a positive value only because of “artificial” monopoly features of the market. Once you “create competition” between landowners, prices fall to input costs, which are zero. 

One detail that many people overlook when they make the “many owners = competition” assumption is that it is simple for even large numbers of people to converge to the monopoly outcome. Trial and error gets you there. In fact, it is not clear that there is a mechanism that gets a market like land away from the monopoly price. Who would deviate?

This is why, for thousands of years, property titles systems have been stores of wealth—an asset traded in markets and subject to cycles like any other asset class. Thinking about land as an asset explains housing price patterns observed much more than any plausible supply-side story. But unfortunately, admitting that the land market is a monopoly is problematic for economists as it undermines many theories (especially involving anti-trust). It also demonstrates that much of our macro-economic policy—monetary policy, taxation policy, and banking policy— is having large effects on housing markets.